the spatial resolution of the human infant visual system
The Spatial Resolution of the Human Infant Visual System
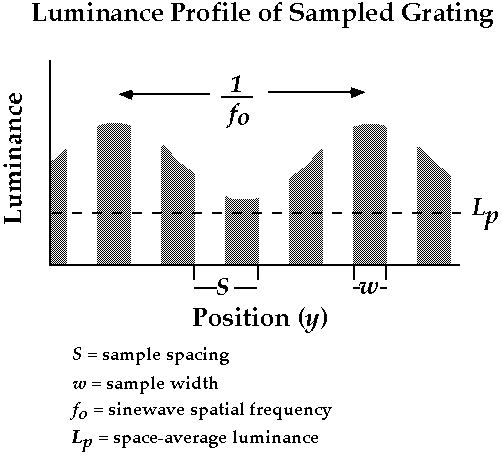
The following sequence of pages describe a problem we investigated in the Banks Lab and present some data from a report in Vision Research (Candy, TR & Banks, MS, 1999). It's well known that the visual acuity and contrast sensitivity of the human infant is very low compared to that of adults. Recent models of human visual development have examined the extent to which infants' low acuity and contrast sensitivity can be understood from information losses among the optics and photoreceptors (e.g., Banks & Bennett, 1988; Wilson, 1988; Banks & Crowell, 1993). We developed a technique that allows one to determine how much the optics and receptors constrain the resolution of the infant system. In particular, we recorded visual-evoked potentials (VEPs) to sampled sinewave gratings, stimuli that generate highly visible distortion products at a nonlinearity early in the retina. The luminance profile of a sampled grating is shown below (this profile shows the variation in luminance as a function of horizontal position in the grating. Unfortunately, it is very difficult to produce a proper sampled grating so we don't have an example of the stimulus for these pages.
sampled sinewave gratings
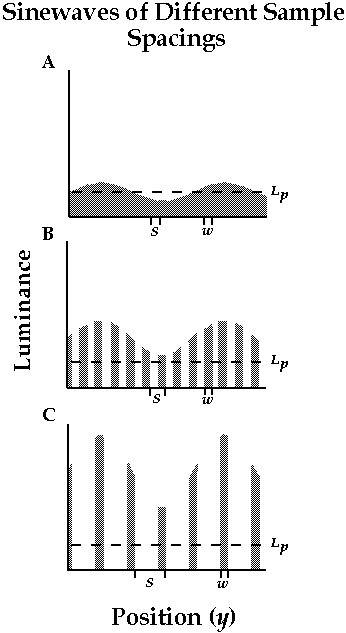
Sampled sinewave gratings were presented to human infants. We varied the the spacing between the samples (S in the last page). As you can see from the figure below, when the sample spacing is small (upper row), the grating is a continuous sinewave. When the sample spacing is large (lower row), the grating consists of widely separated bright bars on an otherwise dark background. With wide spacing, the sinusoidal variation in the brightness of the individual bars is difficult to see. The explanation for this effect is quite interesting.
fourier transform and filtering of sampled gratings
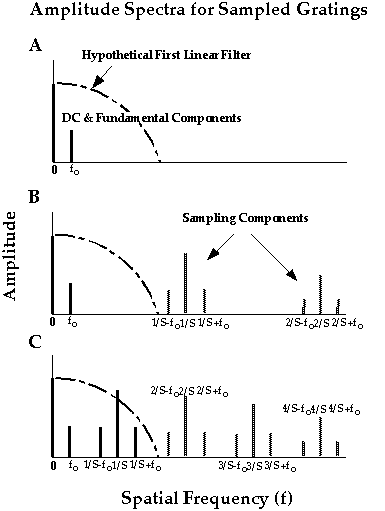
The first stage of visual processing - the optics - is linear. A linear filter does not introduce new spatial frequency components into the stimulus, but a nonlinearity filter does. The figure below shows the Fourier transform of the sampled grating stimulus and the passband of the linear filter (the first filter in visual processing). Amplitudes of the Fourier components are plotted as a function of spatial frequency. Each row displays the amplitude spectra for a different sample spacings (see previous page). The upper row shows the spectrum for a conventional sinewave grating (sample spacing = sample width). The spectrum consists only of a a DC component (related to the luminance) and the Fourier fundamental at f. The middle row is for a stimulus in which the sample spacing is twice the sample width. The spectrum contains the DC component and Fourier fundamental as before, but it now also contains triples of sampling components centered at 1/S, 2/S, and so forth. The spatial frequencies of the sampling components are all higher than the passband of the linear filter, so they do not penetrate this processing stage. The lower row is for a stimulus in which the sample spacing is four times the sample width. The spectrum again contains the DC and fundamental, and triplets of sampling components. The spatial frequencies of the first triplet are now low enough to penetrate the linear filter, so they are passed to the nonlinearity. A compressive nonlinearity creates a distortion product at the fundamental frequency, but 180 deg out of phase with the fundamental. For this reason, the distortion product makes the fundamental harder to see. We used this effect to measure the spatial resolution of the first linear filter (the optics and receptors).
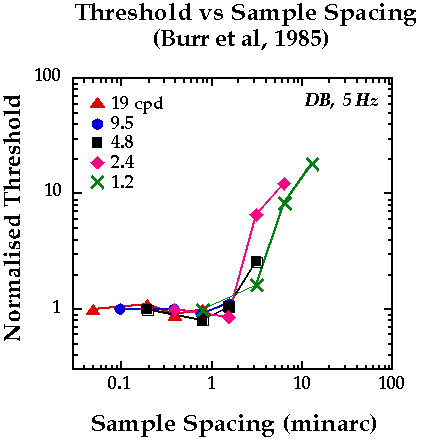
threshold vs sample spacing in adults (Burr et al, 1985)
Burr and colleagues measured adults' ability to detect the sinusoidal variation in sampled gratings. We've replotted their data below. The x-axis is the spacing between samples and the y-axis is the normalized threshold (higher numbers mean less detectable stimuli). Different symbols represent thresholds obtained at different sinewave spatial frequencies. Notice that regardless of the spatial frequency to be detected, the threshold functions take on the same form. Threshold is constant across a range of small sample spacings and then rises steeply as sample spacing is increased beyond a critical value of roughly 2 minutes of arc. We believe that the threshold elevation is a consequence of the distortion product described in the previous page and so the critical sample spacing is a measure of the spatial resolution of the filters before the nonlinearity that creates the distortion. We measured similar functions in human infants.
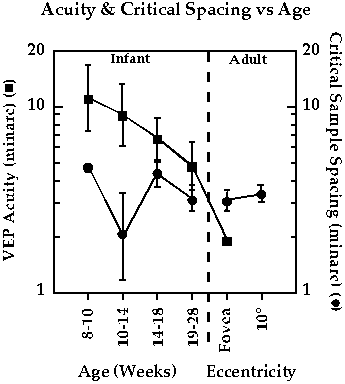
critical sample spacing as a function of age
We used the VEP to measure the critical sample spacing in infants from 8 to 28 weeks of age. The sampled grating stimulus was phase alternated such that the sinusoidal modulation was varied over time but the samples were not. The circles in the figure below show the critical spacing we measured in infants and adults. Notice that they are essentially the same (roughly 2-4 minarc). The squares show the visual acuity at the same ages. These data show that the change in acuity with age CANNOT be accounted for by age-related changes in the resolution of the first linear filter (presumably the optics and receptors). Thus, the cause of the acuity variation with age must be further downstream in visual processing.