Pictures translate a 3-dimensional scene into a 2-dimensional depiction of the scene. As a result of this translation, there is only one viewing location from which the picture will produce the same retinal image as the original scene. This location is called the center of projection. Obviously, when viewing a picture from the CoP, the viewer perceives the scene correctly. From other locations, the retinal image is distorted, but we normally do not notice the changes. A demonstration of the invariance of perceived shape with oblique viewing: View the figure below at a distance of 2 times its height and view it with both eyes. Observe the apparent shapes of the objects. Now rotate the screen ~45 degrees about the vertical axis (left side near). Notice that the objects' apparent shapes do not change much.

The figures below are photographs of the figure on the previous page after rotation; they create approximately the same retinal images generated by the rotated binocular view of the first image. Unlike before, the apparent shapes in these images look quite distorted. Now cross-fuse the images below: the shapes in the fused image appear less distorted. This demonstration shows that perceived shape is determined by more than the retinal-image pattern striking the eyes; it is also affected by the perceived slant of the picture surface.

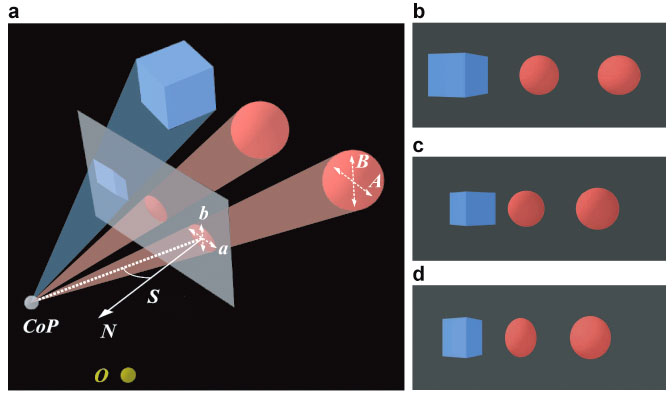
Figure a illustrates the translation from 3-dimensional scene to 2-dimensional picture. Light rays from points in the scene (the cube and two spheres) are "projected" toward the CoP, creating the light field or optic array. The intersection of the light field with the projection plane is the picture. The scene that generated the picture is the depicted scene. The picture reproduces the light field of the depicted scene for a camera or eye at the CoP. Translations and rotations of the projection plane yield different pictures, but the view from the CoP remains the same.

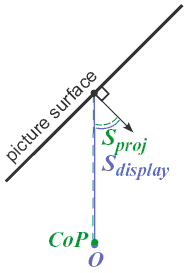
Figures b-d show the similarities and differences between viewing a scene and viewing pictures of the same scene: Figure b is the image seen by a camera placed at CoP. Whether viewing the scene or the picture, the camera's image is the same because the light fields are the same. Figure c is the view of the original scene seen by a camera at O. Figure d is the view of the picture in Figure b seen by a camera at ); it is a double projection, the first occurring in the creation of the picture, and the second with the oblique viewing of the picture. As you can see, the pictures in Figures c and d are quite different. How does the visual system compensate for image distortions resulting from incorrect viewing positions like O?

experiment I

In order to test the explanations of perceptual invariance, we ran experiments in which two kinds of objects were presented: ovoids and slanted planes. With the ovoids, observers reported whether the object was too wide relative to its height to be a sphere. For the slanted-plane task, observers reported whether a rectangular plane rotated about a vertical axis was too wide or too narrow to be a square in the depicted scene. To perform this task veridically, the observer must take into account both the viewing obliqueness and the slant depicted in the picture.

Perspective projection onto a plane produces two effects: foreshortening (stretching of the image in the tilt direction) and scaling (expansion with increasing distance of the projection plane from the CoP).

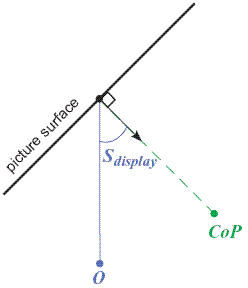
In our experiments, the display could be rotated about a vertical axis through the center of its front surface (Sdisplay). The rotations were as large as 45 degrees, so we could determine whether adjustments for obliqueness occur at large angles.

We also varied the amount of information available for estimating the slant and distance of the display screen: from least informative to most, the conditions were a) monocular viewing through an aperture such that the frame of the screen was invisible, b) monocular viewing without an aperture such that the frame was visible, and c) binocular viewing without apertures such that the frame was visible and binocular disparity was available.

results

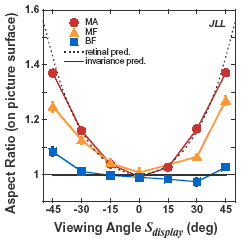
For the ovoid task, the task was to judge whether an ovoid was too wide or too narrow to be a sphere. A staircase adjusted the aspect ratio of the ovoid to determine the ratio that on average looked spherical.

If the observer was invariant for the situation - that is, perceived the projection of a sphere as specifying a sphere for all viewing angles, he would set the aspect ratio on the screen to equal 1, and the data would follow the horizontal solid line in the figure to the right. Alternatively, if the observer did not take the viewing angle into account he only had information from the retinal image. In this case, he would set the object such that is creates a circle on the retina. This prediction is plotted as a dashed line in the figure.

With monocular viewing through an aperture, the observer has very little information about the slant of the display screen. In this condition, ovoid setting followed the retinal predictions (no adjustment for oblique viewing). With binocular viewing, the observer has rich slant information, and settings followed the invariance predictions. With monocular viewing and the frame visible, the data fell in between the retinal and invariance predictions, but closer to the retinal. Thus, frame information had a small effect.

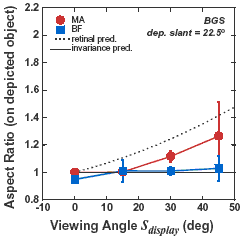
The slanted-plane task yielded similar results. Data was consistent with the retinal predictions when information for surface slant was unavailable and consistent with the invariance predictions when slant information was available. Thus, observers segregated the perspective effects caused by oblique viewing from those caused by picture contents when binocular slant information was available. Compensation does occur.

experiment II

Our first set of experiments determined that compensation for surface slant does occur, but it did not explain how. We next sought to determine whether pictorial or surface information determines adjustments for oblique viewing.

The two hypotheses which we attempted to tease apart are the pictorial-compensation method and the surface-compensation method. The pictorial-compensation method uses geometric information in the picture's contents. Objects with parallel sides, such as cubes, generate vanishing points in the picture. CoP position is recovered from the locations of these vanishing points, three orthogonal vanishing points being sufficient. On the other hand, the surface-compensation method also recovers the CoP position but without using the picture's contents. The viewer assumes the picture is a normal projection, meaning that the CoP is on the central surface normal. The CoP location is determined from a surface slant measurement taken at the middle of the picture. By either method, the retinal image is adjusted to account for the obliqueness of view at various points in the picture once the CoP location is estimated. Pictorial compensation yields geometrically correct compensation in all situations; surface compensation does so only if the picture is a normal projection.

In this experiment, observers again judged aspect ratios of ovoids and slanted planes. However, we altered the projection such that the CoP was not on the central surface normal (in other words, the projection was no longer normal). Rotation of the projection plane does not affect the image seen at the CoP: the same light field is experienced whether one views a frontoparallel projection from the CoP or a rotated projection with the display screen rotated by the same amount. Thus, from the standpoint of the pictorial-compensation hypothesis, changes in the projection angle coupled with changes in viewing angle will not affect percepts. In contrast, the surface-compensation hypothesis predicts large effects of changing viewing angle.

results

Results for the ovoid task are shown here. With binocular viewing and the frame visible, settings followed the surface-compensation predictions. This means that a geometrically correct picture viewed binocularly from the CoP looked distorted when the display and projection screens were rotated. With monocular viewing through an aperture, settings followed the retinal predictions, which means that a geometrically correct picture viewed in this fashion looked undistorted. In the monocular condition with the frame visible, the data were close to the retinal predictions.

To look further for an effect of the geometric content of the picture, we eliminated the cues for vanishing points and redid the ovoid task. The settings with geometric information removed were the same as when the geometric information was maximized. This is inconsistent with the pictorial-compensation hypothesis. In conjunction with the results from the first experiment, we conclude that adjustment for oblique viewing, when it occurs, is based on surface slant and not on geometric information in the picture.

anamorphs

Anamorphs are images that are interpretable only when viewed from a position far from the central surface normal. Usually, we perceive the slant of a picture's surface, and we use this information to compensate for oblique viewpoints. As a result, we end up perceiving something more like the image on the surface than the image on the retina. To correctly perceive an anamorph, the viewer must ignore the surface slant, thus suppressing compensation. By viewing the picture at an extremely oblique angle, the viewer is able to defeat the surface compensation mechanism, and perceive the retinal, and in this case correct, image.

An example of anamorphic art: Hans Holbein's The Ambassadors. When you view from the central surface normal, you see a diagonal smear near the bottom of the painting. When you view with one eye from the right and above the central normal, the smear is perceived as a skull.